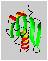 Protein Structure Determination
Protein Structure Determination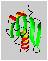 Protein Structure Determination
Protein Structure Determination
Contraints for Structure Calculation
So far, the emphasis has been on identification of the observed
signals in the spectra and their correlation with the amino acid
protons giving rise to the signals. Afterwards, one has to
extract the data which are relevant for the structure. Of
special importance in this respect are proton-proton distances,
which can be estimated from the signal intensities in the
2D NOESY,
3D 15N-NOESY-HSQC and
3D 13C-NOESY-HSQC spectra .
Signal intensity depends on the distance r between two nuclei i and j, according to:
NOEij ~ 1/rij6
Distances are derived from the spectra after calibration against NOE signals for known distances (such as distances in elements of secondary structure) and grouped into a few classes. An upper and a lower bound of distance is assigned to each class. The lower bound is often set to the sum of the van der Waals radii of the two protons.
| NOE class | distance [Å] | upper bound [Å] |
| very strong | 2.3 | 2.5 |
| strong | 2.8 | 3.1 |
| medium | 3.1 | 3.4 |
| weak | 3.5 | 3.9 |
| very weak | 4.2 | 5.0 |
In this procedure, all non-sequential signals which are visible in the NOESY spectra have to be assigned, the number of which easily exceeds 1000 in a medium-sized protein (ca. 120 amino acids). It is distinguished between cross peaks of protons no more than five amino acids apart in the protein sequence (medium range NOE's) and those which are more than five amino acids apart (long range NOE's). The former are mainly indicative of the protein backbone conformation and are used for secondary structure determination, whereas the latter are an expression of the global structure of the protein and therefore contain the main information used for tertiary structure calculation.
In addition to interproton distances the phi-dihedral angles of the protein backbone can be determined from a COSY spectrum or a HNCA-J spectrum (a variant of the HNCA spectrum, from which the coupling constants of the N-Calpha bonds can be determined). Dihedral angles are connected with the coupling constants via the Karplus equation .
So may I invite you all to read his chapter about that topic and return to this page afterwards?
For this purpose, a randomly folded starting structure is calculated from the empirical data and the known amino acid sequence. The computer program then tries to fold the starting structure in such a way, that the experimentally determined interproton distances are satisfied by the calculated structures. In order to achieve this, each known parameter is assigned an energy potential, which will give minimal energy if the calculated distance or angle coincides with its input value. The computer program tries to calculate a structure with a possibly small overall energy.
Without the experimentally determined distance- and torsion angle-constraints from the NMR spectra, the protein molecule can adopt a huge number of conformations due to the free rotation around its chemical bonds (except for the peptide bond, of course). the N-Calpha bond and the Calpha-CO bond. All these possible conformations are summed up in the so-called conformational space. Therefore, it is important to identify as many constraints as possible from the NMR spectra to restrict the conformational space as much as possible, thus getting close to the true structure of the protein. In fact, the number of constraints employed is more important than the accuracy of proton-proton distances, so that the classification above is sufficiently precise.
There are various computer programs, employing two in principle different methods for calculating a protein structure in solution:
Energy Potentials
A starting structure is needed for
a molecular dynamics calculation, which is generated from all
constraints for the molecular structure, such as bond-lengths
and bond-angles. This starting structure may be any conformation
such as an extended strand or an already folded protein. During
the simulation, it develops in a potential field under the
influence of various forces, in which all information about the
protein is summarized. Two classes of energy terms are
distinguished: Eempirical and Eeffective:
V = Eempirical + Eeffective
with:
Eeffective = ENOE + Etorsion,
and
Eempirical = Ebond + Eangle + Edihedral + Evdw + Eelectr
Eempirical contains all information about the primary structure
of the protein and also data about topology and bonds in
proteins in general.
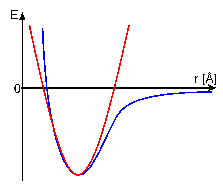 The contributions of covalent bonds,
bond-angles and dihedral angles towards Eempirical are
approximated by a harmonic function. In contrast, non-covalent
van-der-Waals forces and electrostatic interactions are
simulated by an inharmonic Lennard-Jones potential or Coulomb
potential, respectively. Eeffective takes the experimentally
determined constraints into account. Angle constraints are
introduced by a harmonic function analogous to that for the
dihedral angles. For distance constraints, the energy potential
will be set to zero, if the corresponding distance is within the
given limits. If it is outside these limits, a harmonic energy
potential is used, which tries to push the value of the distance
into the limits.
The contributions of covalent bonds,
bond-angles and dihedral angles towards Eempirical are
approximated by a harmonic function. In contrast, non-covalent
van-der-Waals forces and electrostatic interactions are
simulated by an inharmonic Lennard-Jones potential or Coulomb
potential, respectively. Eeffective takes the experimentally
determined constraints into account. Angle constraints are
introduced by a harmonic function analogous to that for the
dihedral angles. For distance constraints, the energy potential
will be set to zero, if the corresponding distance is within the
given limits. If it is outside these limits, a harmonic energy
potential is used, which tries to push the value of the distance
into the limits.
At the beginning of the calculation, the starting structure is energy minimized by moving the atoms of the starting structure, until it reaches an energy minimum. As a result of this process, a structure is obtained which is normally in a local minimum, without satisfying the constraints over vast regions. Such structures cannot reach the global energy minimum by further energy minimization, as they cannot cross the energy barrier between local and global minimum.
However, this energy barrier can be overcome if the necessary energy is put into the system. This is achieved by simulating the heating of the system up to a few thousand Kelvin via a coupled temperature bath. At this temperature the system receives enough energy to cross the energy barrier. Now, the system once again develops in energyhyperspace under the influence of the potential field.
The atomic positions at the end of a simulations step are determined from their starting positions, as well as from their velocities and accelerations, which in turn are both derived from the starting positions. Velocities can be calculated from the Maxwell distribution at a given temperature and accelerations are determined by Newton's equation from the force field. After a simulation step the energy potential is recalculated for the new atomic positions and a further simulation step follows. This procedure is iterated, searching the energyhyperspace for a global minimum.
After a previously chosen number of simulation steps at high temperature (up to 6000 times), atomic velocities (i.e. temperature) are slowly reduced in many steps (usually ca. 3000). At each temperature, the system is once again left to develop under the influence of the potential field. While the temperature of the system is reduced, simultaneously the force constants in the experimental constraints are raised in order to weigh them more strongly.
The result of the simulation is a minimum energy protein structure, but it cannot be excluded that this structure is stuck in a local minimum without ever reaching the global minimum, which is only marginally lower in energy. Therefore, about twenty different starting structures with random folds are used, which reach their final structure via different paths in energyhyperspace. These resulting structures are iteratively re-used as starting structures for another SA with slightly changed input protocolls, until no further reduction in global energy is observed and the structures converge in conformational space.
The RMSD is different for different parts of the protein structure: Regions with flexible structure or without secondary structure (loops) show a larger deviation than those with rigid and well defined secondary structure. This higher RMSD in loops results in first instance from the smaller number of distance constraints for these parts of the protein structure. Additionally it can originate from real flexibility, but this diagnosis can only be confirmed by measuring the relaxation times for the protein.
A result of a structure calculation is shown here:
This MOLSCRIPT-picture (suitable for stereo viewing) shows a ribbon plot of the averaged structure of the protein DS111M.
![]() You can also view this structure with RasMol:
You can also view this structure with RasMol:
Here is the pdb file (126k) of the averaged structure of severin.
Try this rasmol script to viev the protein backbone colored according to secondary structure.
The following stereo picture shows the family of the 20 final structures of the protein DS111M:
Only the backbone atoms are shown in this picture for the sake of clarity. The orientation of the molecule is the same as in the picture above.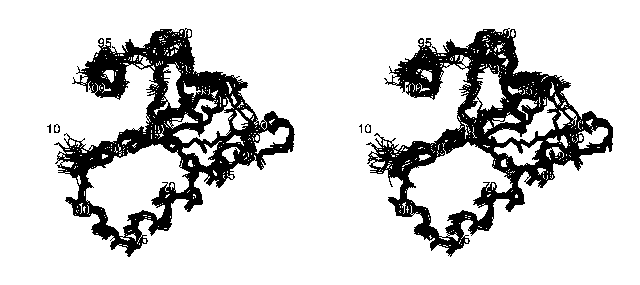
The accuracy in this family of structures can be displayed by another method: The following picture shows the backbone of DS111M as a cylindrical "sausage" of variable radius, which represents the global displacements among the 20 model structures in the structural family:
![]() If you like to see it with rasmol
here is a
pdb file (2.3 MB!) with the family of 20 structures
of severin.
If you like to see it with rasmol
here is a
pdb file (2.3 MB!) with the family of 20 structures
of severin.
Try this rasmol script to viev only the protein backbone of the structures colored with ramol standard colors according to secondary structure.
The calculation of this structure was performed with 1011 distance and 55 torsion angle constraints. This example illustrates the importance of a large number of constraints for obtaining a well defined NMR structure.