 One Dimensional NMR Spectroscopy
One Dimensional NMR Spectroscopy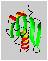 One Dimensional NMR Spectroscopy
One Dimensional NMR SpectroscopyEach 1D NMR experiment consists of two sections: preparation and detection. During preparation the spinsystem is set to a defined state. During detection the resulting signal is recorded. In the simplest case the preparation is a 90° pulse (in our example applied along the x axis) which rotates the equillibrium magnetization Mz onto the y axis (My). After this pulse each spin precesses with its own larmor frequency around the z axis and induces a signal in the receiver coil. The signal decays due to T2 relaxation and is therefore called free induction decay (FID).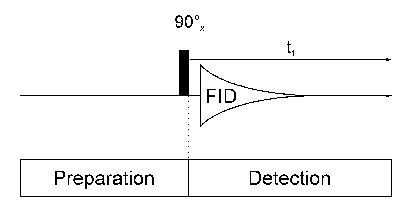
Usually, the experiment is repeated several times and the data are summed up to increase the signal to noise ratio. After summation the data are fourier transformed to yield the final 1D spectrum.
I will use this 1D spectrum of Ethanol as an example for the discussion of several spectral parameters. The spectrum contains three signals two of wich are in part split up into several lines (the split signals are called multipletts). The three signals can be assigned to the OH, CH2 and CH3 protons, respectively. The three methyl protons are equivalent to each other and give only one signal. The same is true for the two methylene protons. The number of protons which cause a specific signal can be calculated by integration over the signal: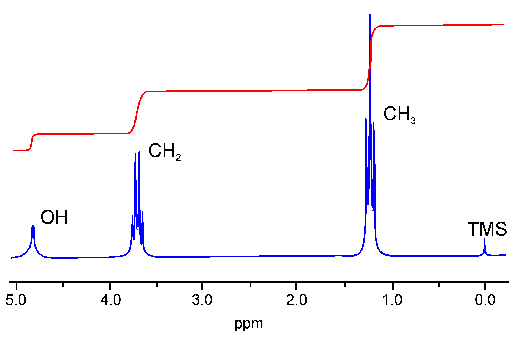
The value of a signals chemical shift (delta) in ppm (parts per million) is defined as:
delta = ((wsignal - wreference) / wreference) * 106
The unit ppm is used instead of Hz because the former is independent of the magnetic field strength B0. The reference frequency for the ppm scale is the signal of the methyl groups of tetramethylsilan (TMS, the chemical shift of which is defined as 0 ppm). In protein NMR the substance DSS (2,2-dimethyl-2-silapentane-5-sulfonic acid) is used equivalently.
Different chemical groups have different chemical shifts. This is one of the major information sources in NMR spectra. In proteins, for example, the signals of HN, Halpha, aromatic and aliphatic protons can be distinguished by their chemical shift. Additionally the chemical shift contains information about protein secondary structure.
The distance of the lines in a multiplet (in Hz) is given by the coupling constant J which is independent of the magnetic field strength. Normally, couplings over one (1J) two (2J, geminal coupling) and three bonds (3J, vicinal coupling) are observed. Vicinal couplings depend on the torsion angle between the coupling protons. This is described by the famous Karplus equation: J(phi) = A * cos2(phi - 60) - B * cos(phi - 60) + C
Therefore, it is possible to derive parts of the molecular geometry from the knowledge of coupling constants.