Theory of NMR Spectroscopy
Theory of NMR Spectroscopy
Of course, this picture is a classical model whis has nothing to do with reality. The quantum mechanical property 'spin' does not mean that the nucleus is spinning around ist own axis (if it did its radial speed would be greater than the speed of light). It is therefore an unfortunate choice of words if we denominate the spin as the angular momentum of a nuleus, because spin is a pure quantum mechanical property which could as easily be called 'happiness' or 'peppermint flavor'.
The spin is quantized according to
J = h/(2pi) * sqrt(I(I+1))
with J being the spin angular momentum, I the spin quantum number (which can have values of I=0,1/2,1,3/2,...,6. By convention it is simply called 'spin'.) and h the planck's constant. The angular momentum and the magnetic moment are directly proportional:
µ = gamma * J = gamma * h/(2pi) * sqrt(I(I+1))
The constant gamma is characteristic for each isotope and is called the gyromagnetic ratio. The sensitivity of a nucleus in NMR depends on gamma (high gamma, high sensitivity).
In an external magnetic field the magnetic moment orients according to:
Jz = - m * h/(2pi) => µz
= m * gamma * h/(2pi)
The magnetic quantum number m can be an integer number between -I and +I. Thus, the external field leads to a splitting of the energy levels. For spin 1/2 nuclei (e.g. protons, see table) two energy levels exist according to a parallel or antiparallel orientation of the magnetic moment with respect to the magnetic field:
The energy of these levels is given by the classical formula for a magnetic dipole in a homogenous magnetic field of the strength B0: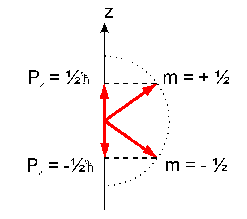
E = - µz * B0
= - m * gamma * h/(2pi) * B0
The magnetic moment of each nucleus precesses around B0. The frequency of this precession is the larmor frequency (w0) which is equivalent to the resonance frequency of the nucleus and the energy difference between the two levels.
gamma * h/(2pi) * B0 = DELTA E = h * nu
= h/(2pi) * w0
=> w0 = gamma * B0
The larmor frequency depends on the gyromagnetic ratio and the
strength of the magnetic field (see picture), i.e. it is different for each
isotope. At a magnetic field of 18.7 T the larmor frequency of
protons is 800 MHz.
The excited spins emit the absorbed radiation after the pulse. The emitted signal is a superposition of all excited frequencies. Its evolution in time is recorded. The intensities of the several frequencies, which give the observed signal in their superposition, are calculated by a mathematical operation, the Fourier transformation, which translates the time data into the frequency domain. The resulting NMR spectrum looks like an ordinary cw spectrum but its resolution is several orders of magnitudes better.
Andrew Derome suggested in his book
[5]
the following analogy for FT-NMR which
is really beautiful:
The FT method can be compared to the tuning of a bell. In
principle, you could measure each of the tones which make up the
sound of a bell in a 'cw experiment': Excite the bell with all
frequencies from the deepest tones to the edge of ultrasound and
measure the reaction of the bell with a microphone. But this
method is extremly complicated and every bell founder knows a
much faster way: Take a little hammer (or perhaps a bigger one)
and - BOIIINGGGG.....
The sound of the bell contains each tone
at the same time an every person can analyse it directly with
his or her ears (wich are a cleverly 'constructed' instrument
for FT). The advantages of this 'pulse FT method' over the 'cw
method' are clearly obvious.
Np / Nap = exp (DELTA E/(kT)) = exp (gamma * h/(2pi) * B0 / (kT))
Both energy levels are nearly eqally populated, because the
energy difference is in the order of magnitude of thermic
movements (kT). At T=300 K and a magnetic field of 18.7 T (800
MHz) the excess in the lower enery level is only 6.4 of 10000
particles for protons. This is the main reason for the
inherently low sensitivity of NMR when compared to optical
spectroscopic methods.
The magnetic moments of the individual spins sum up to a macroscopic magnetization M0 which can estimated according to Curie's law:
M0 = N * gamma2 * (h/(2pi))2 *
B0 *I(I+1) / (3kT)
=> M0 = N * gamma2 * (h/(2pi))2 *
B0 / (4kT), with I=1/2
It is the evolution of this macroscopic magnetization which is
recorded in the spectrometer. The classical theory of NMR also
deals with this quantity. In thermal equillibrium only
magnetization along the axis of the magnetic field exists (by
definition z), because the x and y components sum up to zero.
This concept should be very familiar to us, because we all live in a rotating coordinate frame - the earth. To an observer in a spaceship a person 'standing' on the equator is moving at a speed of about 1700 km/h. A ball which is thrown 'vertically' up in the air comes down again in a straight vertical line. However, our observer in space sees this ball moving on a complex parabola.
Mathematically, the time dependency of the macroscopic magnetization M is described by the Bloch equation:
dM/dt = gamma* [M × Beff]
Beff = (B0 + (w0/ gamma)) + B1 = B1
--------------The time dependecy of the magnetization vector M results from the interaction of the magnetization with the effective external magnetic field Beff. In the rotating frame the contribution of B0 to Beff is cancellled out (for nuclei with the larmor frequency w0), i. e. Beff equals zero as long as only the static external field B0 is applied.
=0
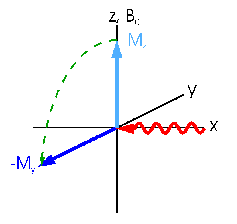Transversal magnetization (dark blue)
can now be created by applying an additional magnetic field B1 (red)
which is perpendicular to B0. This B1 field is the
radiofrequency pulse mentioned above. If the radiation frequency
is equal to the larmor frequency of the nuclei the field causes
a rotation of the equillibrium magnetization Mz (light blue) around the x
axis (cross product, Beff=B1).
You can completely transform the
z magnetization to y magnetization if the duration of the pulse
is sufficiently long. In this case the pulse is called an
'excitation pulse' or '90° pulse' (obviously because the
rotation angle of the magnetization is 90°).
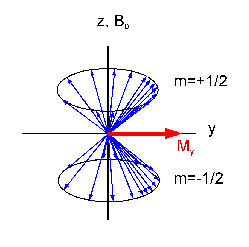The state of x (or y) magnetization can be explained in the single spin
model: The two energy levels explained above are equally
populated (Mz = 0). Additionally, the magnetization dipoles
of the spins are not statistically distributed around the z
axis. A small part of them precesses 'focussedly' in phase
around the z axis. They sum up to the macroscopic x
magnetization. Therefore, states with transversal magnetization
are also called 'phase coherence'.
dMz/dt = gamma * [M × Beff]z + ((M0 - Mz)/T1)
dMx,y/dt = gamma * [M × Beff]x,y - (Mx,y/T2)
T1 and T2 are called the longitudinal and transversal relaxation times, respectively. The transversal components of magnetization (Mx, My) approach zero whereas the longitudinal component Mz approaches M0 with time. Relaxation is caused by several time dependent interactions between different spins (T2) and between spins and the surrounding lattice (T1). Therefore, T1 is also called spin-lattice relaxation time and T2 spin-spin relaxation time.
[Introduction]
[Index]
[PPS2 Projects]
[1D NMR Spectroscopy]
