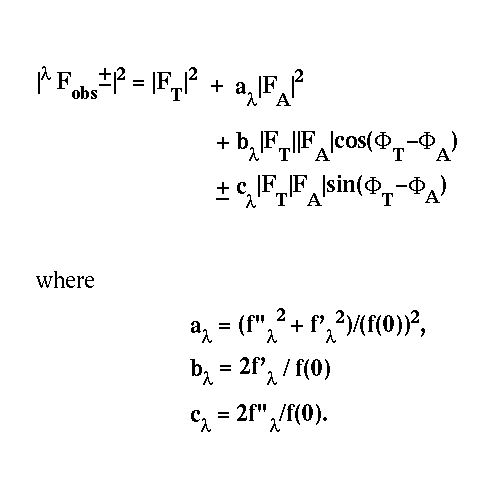
Phase problem in macromolecular crystallography |
Introduction
In a X-ray diffraction experiment one can only measure the intensities and diffraction angles of the diffracted beams. The relative phases are lost in the process in all usuall diffraction experiments. This loss phase information along with the amplitudes of the diffracted X-rays is essential for the solution of crystal structures and is referred as the phase problem. There are three popular approaches which may be taken in recovering phase information in a diffraction experiments - molecular replacement (MR), multiple isomorphous replacement (MIR) and multiwavelength anomalous diffraction (MAD).
Molecular Replacement
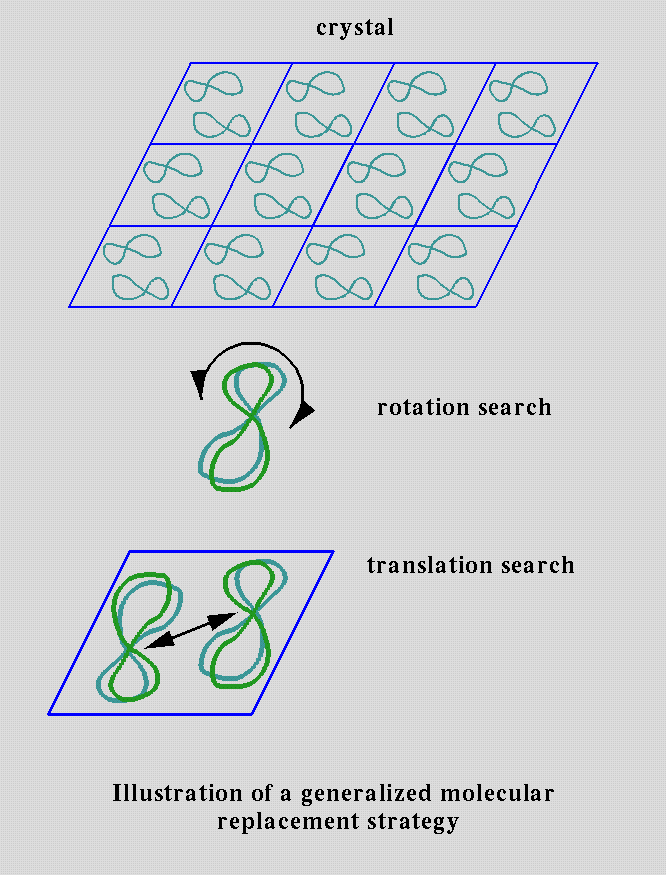
If a related or homologous (more than 50% sequence identity) protein structure is already known then the method of Molecular Replacement (MR) may be used. The idea is to find the rotation and translation which position the model structure in the unit cell so as to give the highest correlation between experimental diffraction measurements and those calculated from the model.

The basic ideas were desribed by Michael G. Rossmann and David M. Blow in 1962. [1,2]
Multiple Isomorphous Replacement (MIR)
The most common method of ab initio phase determination for proteins is Multiple Isomorphous Replacement (MIR) - introduced 40 years ago [3-5]. MIR involves introducing heavy atoms into protein structure. Heavy-atom derivatives are prepared by soaking the native protein crystals in a buffer containing heavy-atom compound or by cocrystallization The native and heavy-atom derivative crystals should be isomorphous - crystal form and unit cell dimensions should be unchanged. The structure factors of heavy-atom derivative (ph) and native protein (p) and heavy atom (h) have the following relationship:
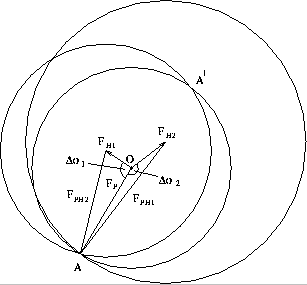
If the magnitudes |Fph| and |Fp| are measured experimentally and |Fh| and phase angle are obtained from the heavy-atom model. Only one heavy-atom derivative (single isomorphous replacement - SIR) gives two possible solutions for the phase of Fp. One of these is the true solution.
Using second heavy-atom derivative (ph2) with a different position, a unique solution can be obtained as shown in a geometric representation [6]
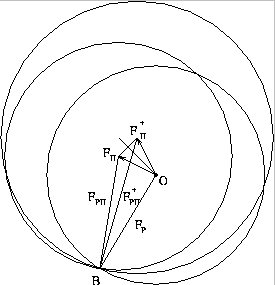
A similar vector construction also can be produced by anomalous dispersion.
Multiple Wavelength Anomalous Diffraction (MAD)
The theory of MAD was developed as early as that of MIR. In MAD changes are induced in the atomic scatering factor of a heavy-atom bound to protein by measuring diffraction data at a number of different X-ray energies where the anomalous scattering factors of the heavy atom are significantly different from one another. The largest changes in the anomalous scattering factors of atoms occur around characteristic absorption edges since their values are directly related to the atoms atomic absorption coefficient. This is convenient since the majority of heavy atoms which bind to proteins have absorption edges which lie in the energy range typically used for protein diffraction work (5-20 keV).
Information about the phase of the scattered X-rays can be
derived from the resonance effects or anomalous scattering. Anomalous scattering is an
atomic property and thus thus enters the equations for X-rays diffraction in the expression
for the atomic scattering factor (f), which is the sum of "normal" atomic
scattering factor f(0) and a complex anomalous cortrrection having real (f')
and imaginary (f") components:
Wavelength-tunable synchrotron radiation allows the real component (f') to be used
as well, providing the opportunity for direct phasing through combination of orthogonal
effects of f' and f".
The formulation of the MAD observational equation is based on that of Karle
[7] and modified by Hendrickson [8]:
The MAD observaional equation involves no approximation, and the accuracy of MAD
phases is limited only by the precsion of the diffraction data. This is in contrast
to MIR where the phase accuracy by breakdown of the assumption of isomorphism of
native and derivative crystals [9]
f = f(0) + f' + f"