Symmetry is the concept of repetitive arrangements of similar objects in space. The space we are interested in is normal Euclidean 3-dimensional space, although symmetry can be studied in any number of dimensions. For instance, it may be shown that there are just seventeen ways of arranging two-dimensional objects on a plane using regularly repeated combinations of the operations translation, rotation, mirror-reflection and glide-reflection. These possibilities produce what are known as the `Wallpaper Symmetries'.

In three dimensions, three-dimensional objects may be arranged in a considerably larger number of ways, and many of these are exhibited in crystal forms. Again, each possible arrangement is achieved by a combination of simple, basic operations. These include translation, rotation, screw-rotation, mirror, inversion, inversion-rotation, and glide-reflection. The total number of possible ways of arranging copies of the same object to form a repeating lattice in 3D-space can be shown to total 230. These are the `Space Groups' familiar to crystallographers. They are enumerated and detailed in The International Tables of Crystallography.

Now, proteins are chiral objects, and cannot be mirror-inverted whilst remaining the same. Their mirror reflection is DIFFERENT. Thus, many of these arrangements are actually precluded. In fact, proteins may only adopt 65 of the 230 possible 3D space groups. Many of these are observed when we crystallise proteins.

In the case of naturally occurring multimers of proteins, other constraints occur which limit the possible arrangements. We are speaking here of individual assemblies of monomer units, creating (usually soluble) complexes which exhibit internal symmetry.

Thus, the monomers must associate with van der Waals contact interfaces between the sub-units of the assembly. But, the sub-units cannot intersect. They may interpenetrate only in so far as there exist corresponding `knobs' and `holes'. Furthermore, axes of purely rotational symmetry may not actually pass `through' a protein monomer.

This leads to the limited possibilities enumerated and illustrated below.

Protein Multimer Symmetry

Cyclic symmetries

VERY common - examples include horse-liver alcohol dehydrogenase , growth factors,

Examples include chloramphenicol acetyltransferase (pdb, gif1, gif2, gif3, gif4), and glucagon (1GCN)(Exercise: Create the trimer)

We were unable to find any examples of this. Can anyone enlighten us?

Examples include serum amyloid P-component (pdb, gif1, gif2)

Higher Cyclic symmetries observed include

eg C-reactive protein from the horse-shoe crab (Limulus)

Heptamers

Octamers

eg Light harvesting complex

Decamers

er . . .

Undecamers

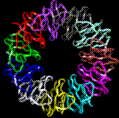TRAP Trp attenuation protein of Bacillus subtilis

Dihedral symmetries

Examples include lactate dehydrogenase (pdb, gif), glyceraldehyde dehydrogenase (pdb, gif1) gif2), Fe or Mn superoxide dismutase ( pdb, gif1, gif2)

Examples include

Examples include hemerythrin ( pdb, gif1, gif2)

eg glutamine synthetase ( pdb, gif1, gif2, gif3)

GroEL

Higher symmetries

Octahedral

Tetramer of Trimers (Tetrahedral)

Icosahedral symmetry- exhibited in many viruses

References

• Voet, D. and Voet, J.G. (1990) Biochemistry, John Wiley and Sons, New York
• Klotz, L.M., Klippenstein, G.L., & Hendrickson, W.A. (1976) Science 192, 335-344
• Cooper, J., McIntyre, K., Badasso, M., Wood, S., Zhang, Y., Garbe, T. & Young, D. (1995) J.Mol.Biol. 246, 531-544

Back to Main PPS Index
Alan Mills & J. Walshaw