Back to main Molecular Forces index
Back to previous unit Non-bonded Interactions
On to next course unit Potential energy functions and simulation methods
The fact that proteins normally function in an aqueous environment considerably complicates the understanding of the interactions between different groupings. We have already seen that when thinking about the effect that various interactions (such as hydrogen bonds) have on the overall stability of a protein one must compare the free energy contribution to the folded state with that of the random coil. In this section we will examine further two important contributions that solvent makes to protein interactions.
When two charges interact in a vacuum the energy of their mutual interaction is given by Coulomb's law:
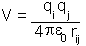
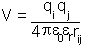
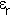 is the dielectric
constant or to use the modern but little used alternative term
relative permittivity. The following table quotes the value of
the dielectric constant measured for a number of materials.
is the dielectric
constant or to use the modern but little used alternative term
relative permittivity. The following table quotes the value of
the dielectric constant measured for a number of materials.The dielectric constant of selected materials
Material Dielectric constant
Water (20oC) 80.3 Water (0oC) 87.7 Ice polycrystalline (-10oC) ~98 Methanol 33.6 Liquid H2S (-85.5 oC) 9.3 Beeswax 2.9 Paraffin 2.0-2.5 Liquid Argon (-191oC) 1.5 Vacuum 1.0 (by definition)
(At zero frequency and room temperature unless otherwise indicated
Source: CRC handbook except for ice value from
Fletcher, N.H. (1970) The chemical physics of ice CUP, Cambridge)
The source of dielectric effects is that the electric field polarizes the material involved. Suppose that we have two charges interacting in a vacuum. We can draw the electric field lines (the direction in which a positive charge would be forced to move) thus:
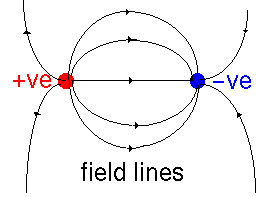
So we have seen that the dielectric constant of materials is caused by microscopic dipoles in the material. These have two sources:

So we can begin to understand the figures quoted for the dielectric constant in the table above. Water has a very high dipole moment (as mentioned in section on hydrogen bonding) due to the electronegativity of oxygen and the fact that hydrogen-oxygen bonds are short. So it has a high dipole moment. In methanol one of the hydrogen atoms is replaced by a CH3 group lengthening the bond and so reducing the dipole moment and consequently the dielectric constant by a factor of over 2. For H2S the oxygen has been replaced by the much less electronegative sulphur atom and the bond lengths have been increased. As already mentioned this has the result that the compound is unable to form hydrogen bonds and is a gas at normal temperatures/pressures. Not surprisingly when liquefied its dielectric constant is one eighth that of water.
Going down the list we find that organic essentially unpolarized compounds have a dielectric constant of around 2 to 3 - this will be around the value found in lipid bilayers. The contribution to this of electron polarization can be estimated by comparison to liquid argon with a dielectric constant of 1.5.
That the dielectric constant of ice is around 100 surprises many people (including the author). Although ice is crystalline with the oxygen atoms confined to a tetrahedral pattern, Bernal and Fowler showed the dipole moments of individual water molecules to be randomly orientated. The crystal does not have any restraining effect on their ability to reorient in an electric field (for further details see reference to Fletcher's book above).
So what implications does this have for interactions of importance to proteins? The first thing to note is that the concept of a dielectric constant is an essentially macroscopic concept. That is that relies on the fact that the space around the charges is uniformly filled with a large number of small dipole moments or polarizable atoms. As the separation of the charges is reduced to the same scale as the molecules which produce the dielectric effect this assumption breaks down. The medium surrounding two interaction will have some dielectric effect but it will not be as simple as a constant.
In the early days of protein simulation (1980's) it was often assumed that the effective dielectric "constant" between two charges at a separation of R angstroms varied as R. This had the fairly dodgy justification that one could expect electronic polarizability to dominate when two atoms are in proximity, when R is around 3 (not necessarily true as the medium surrounding the charges as well as between them has a dielectric effect). At large distances the dielectric would get larger reflecting the fact that increasing amounts of water would tend to surround the charges. The real justification for the model was that it save a lot of computer time when this was a really scare commodity. It changes Coulomb's law into a R-2 dependence so that it avoids the necessity of finding using the square root to work out the distance between two atoms. Recent work has found that using a more sophisticated function to represent "dielectric constant" (usually with a sigmodial form) has yielded good results.
A more normal approach today is to actually include a large number of water molecules in a molecular dynamics simulation. A dielectric constant of 1 or 2 (to represent electronic polarizability) is used. An alternative approach is to use a "reaction field".
(a bit on Poisson-Boltzmann based techniques could be placed
here).
This is in essence a simple observation that a apolar molecules tend to aggregate in the presence of water. It is known to be entropically rather than enthalpically driven. For this reason it is not usual to incorporate a term for hydrophobic energy into potential energy functions. In fact simulations can be performed using molecular dynamics methods showing hydrophobic aggregation for small molecules using a conventional potential energy function (see Wallqvist, A (1991) "Molecular dynamics study of hydrophobic aggregation in water/methane/methanol systems" Chem. Phys. Lett. 182:237-241)
The hydrophobic effect is of great importance to protein folding for further details see Advanced topic: "The hydrophobic effect and protein unfolding" (contribution from John Walshaw).
On to next course unit Potential energy functions and simulation methods