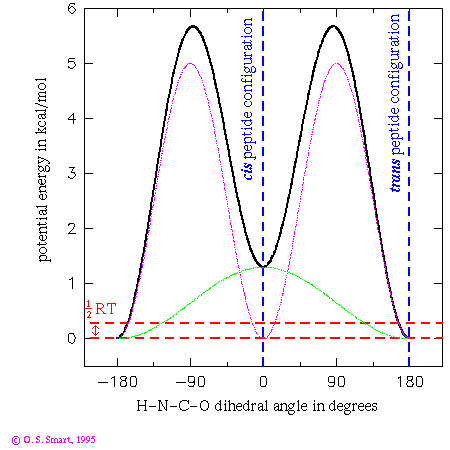
This graph shows the potential energy for a H-N-C-O dihedral angle the Pitzer potential:
Back to main Molecular Forces index
Back to main PPS course Index

This graph shows the potential energy for a H-N-C-O dihedral angle the Pitzer potential:
![E_dihe= sum_(i=1)^n (V_n/2)*[1+cos{n.phi-gamma}]](os_dihe.gif)
The parameters used are from the AMBER potential energy function:
nAs you can see only of two of the three terms have a non-zero barrier height. This leads to an effective functional form:(in kcal/mol)
(in degrees) 1 1.3 0. 2 5.0 180. 3 0.0 -
![0.65[1+cos(phi)] + 2.5[1+cos(2phi-180)]](os_di_om.gif)
where 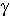 is the H-N-C-O dihedral angle
in degrees. The first term leads to an energy dependence shown by the
light green line in the graph and the second leads to the purple/pink line.
Added together they lead to the thick black line - giving the potential
energy dependence for the dihedral angle change. By the use of
a three term Fourier series complex energetic behaviour can be
modelled.
is the H-N-C-O dihedral angle
in degrees. The first term leads to an energy dependence shown by the
light green line in the graph and the second leads to the purple/pink line.
Added together they lead to the thick black line - giving the potential
energy dependence for the dihedral angle change. By the use of
a three term Fourier series complex energetic behaviour can be
modelled.
The practical consequence of these terms is to ensure that the peptide bond is planar during an energy minimization or molecular dynamics run. Note that the trans configuration for the peptide bond is favoured over the cis form by 1.3 kcal/mol. The dashed red lines indicates an energy of 0.29 kcal/mol which is equal to 1/2RT at a temperature of 300K. This is the energy that an individual degree of freedom can expect at this temperature: one can expect that it would be most unlikely for an individual peptide to surmount the energy barrier of over 5 kcal/mol to flip from a cis to trans conformation. Experimentally it is most unusual to find a peptide other than a proline in a cis conformation.

<li>CA-C-N-CA (marked in yellow)
<li>O-C-N-CA (marked in green)
</ul>
in the <a href=os_pef.html#amber>AMBER</a> potential energy function
each one of these dihedral angles will have a contribute to the
total potential energy. All three will have the parameters:
<pre>
n <img alt=) (in kcal/mol)
(in kcal/mol)  (in degrees)
1 0.0 -
2 5.0 180.
3 0.0 -
Therefore for each of these dihedral angles will be equal to the
purple/pink line shown on the graph above.
The three atoms bonded to the N atom are co-planar (all the bond
angles are 120 degrees) - this
also the case for the three atoms bonded to the C atom. This
means that all four dihedral angles will be either (almost exactly)
in step with one another or differ by 180 degrees. As each contributes
an energy dependence as shown by the pink line they will "constructively
interfer". Thus the barrier to rotation of the omega dihderal angle
will be increase to over 20 kcal/mol (as suggested to be appropriate
by Schulz & Schimer). However, as the other three dihedral angles
do not have any n=1 term they do not effect the cis-trans
energy difference.
(in degrees)
1 0.0 -
2 5.0 180.
3 0.0 -
Therefore for each of these dihedral angles will be equal to the
purple/pink line shown on the graph above.
The three atoms bonded to the N atom are co-planar (all the bond
angles are 120 degrees) - this
also the case for the three atoms bonded to the C atom. This
means that all four dihedral angles will be either (almost exactly)
in step with one another or differ by 180 degrees. As each contributes
an energy dependence as shown by the pink line they will "constructively
interfer". Thus the barrier to rotation of the omega dihderal angle
will be increase to over 20 kcal/mol (as suggested to be appropriate
by Schulz & Schimer). However, as the other three dihedral angles
do not have any n=1 term they do not effect the cis-trans
energy difference.
 Section under construction.
Section under construction.
MORE TO BE ADDED WHEN NON-BONDED SECTION WRITTEN!
Return to looking at dihedral angle interaction