Advanced topic: A brief introduction to quantum chemistry

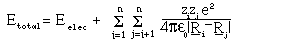
(c) O.S. Smart 1995, all rights reserved

This section is adapted from part 1.2.2. of O.S. Smart, "Simulation of a conformational rearrangement of the substrate in D-xylose Isomerase", University of London Ph.D. thesis (1991).

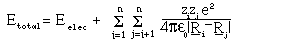
where R_i are the position vectors of the nuclei and the Z_i the charges. The electronic wavefunction and potential energy are given by:

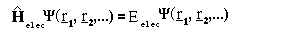
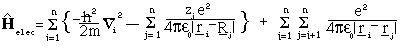
where r_i are the position vectors for the electrons.

In the case of the simplest molecule 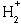the exact solution can be found numerically, but with some difficulty (Wind, H., 1965, J. Chem. Phys. 42:2371-2373). In more complicated systems, it is necessary to take a different approach. The LCAO method, which is commonly used, expresses a trial molecular orbital (MO) as a Linear Combination of the individual Atomic Orbitals 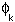for the molecule:

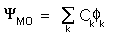
The variation principle can be exploited to find values for the coefficients 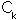. The principle states that the expectation value 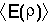. of a Hamiltonian calculated with any function :

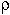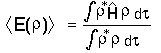
must lie above the true ground state energy (the integration is over all space). Or put another way if we have a trial wavefunction for the molecule and we make a change which lowers the energy then the new function is a better approximation to the true wavefunction to the system. Thus, the optimal value for the coefficients 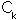can be found by adjusting the coefficients so as to minimize .

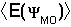A further complication arises because of the last term of the Hamiltonian which describes electron-electron repulsion. Without this term it would be possible to use the method of separation of variables to solve the Schrödinger equation independently for each electron, but this is not possible when the term is taken into consideration. The standard approximation, developed by Hartree and Fock, to avoid this problem is to assume that each electron moves in the average field due to the nuclei and the other electrons. An initial set of wavefunctions is guessed for the molecule. In the LCAO approach a series of fixed phi called the basis set, is chosen (this must at least give a representation for each occupied atomic orbital of each atom) and the initial guess is a set of coefficients C_k (n.b. this must satisfy the Pauli principle and be antisymmetric - see Hinchliffe). The optimal coefficient for each atomic orbital in turn is found while keeping the other orbitals frozen. The procedure is continued until all the coefficients remain unaltered in a pass through the cycle and become self-consistent. The method is known as the self-consistent field approach (SCF).

This is commonly known as ab initio simulation and has the great advantage that a molecule can be treated without the need for any empirically derived parameters. The accuracy is reasonable (providing a basis set of a reasonable size is used) and methods exist to reduce the errors caused by the SCF approximation, by considering electron correlation in the calculation (see Hinchliffe). The geometry of a model can be improved by calculating the energy for a series of nuclear positions, and using an energy minimization procedure (i.e., varying R_i so as to minimize the potential energy). Its great problem lies in its c.p.u. cost: which rises by approximately n to the power 3.5 where n is the number of basis functions used for the calculation. Therefore, it is very expensive to improve the accuracy of a simulation for a small molecule, or to model a larger molecule. The practical limit of the calculation is a few tens of atoms (Weiner et al., 1984; Singh and Kollman, 1984). Semi-empirical quantum simulations (such as AM1: Dewar et al. , 1985), in which approximations and empirical data are introduced into SCF calculations allow this limit to be extended. However the techniques are far too expensive to be applied to the smallest protein.

or the advanced topic: The application of quantum chemistry to protein simulation. (also contains references for this section).

Back to the Top