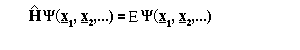
On to next course unit Covalent Interactions
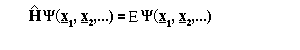
where x are the positions of the nuclei and electrons of the molecule, 'Psi' is the wavefunction which contains all information about the dynamical properties of the system and E is the energy for the state. The Hamiltonian operator is given by:
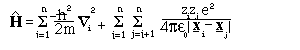
Where m_i is the mass of particle i, Z_i the charge and the other symbols have their conventional meaning. The former term equates to the classical kinetic energy and the latter to the electrostatic (Coulomb) energy. Do not worry too much if you do not understand the equation! - it is just important to know that it exists. The properties of all molecules, including proteins, are governed by this equation (excluding the small effects due to relativistic considerations). Unfortunately the solution of this equation is not possible even for simplest molecule H_2^+ (i.e., two protons and an electron), without making an approximation
Subject to the approximation, the energy for a molecule
of N nuclei and n electrons is given by:
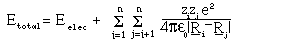
where R are the position vectors of the nuclei and the Z_i the charges. The first term represents the contribution made to the potential energy by interactions involving the electrons, the second is simply a classical Coloumb term giving the replusive interaction between the charged nuclei of the molecule. The electronic wavefunction and potential energy are given by:
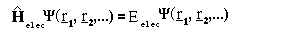
The Hamiltonian operator for the electrons' contribution to the energy is given by:
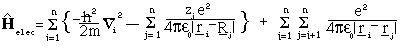
where m is the mass of the electron and r_i are the position vectors for the electrons. The first term of the sum corresponds to the kinetic energy of the electrons, the second the interaction between electrons and nuclei and the third the (tricky) electron-electron interactions.
The basic idea of quantum chemical methods is to find
the electron distribition for a fixed set of
nuclear positions describing the molecule (see the
Born-Oppenheimer approximation ).
By the application of an
energy minimization procedure the geometry of the
molecule can be optimized.
Suppose one could solve the Schrödinger equation for all the nuclei and electrons in the system of interest (e.g., an enzyme, its substrate and a surrounding set of water molecules) for any given set of nuclear positions. If this could be done in a reasonably short time then allied with molecular dynamics (and other techniques) it would be possible to fairly comprehensively treat the structural properties, dynamics and chemical reactions of a protein from first principles.
Unfortunately, it is impossible apply the methods to molecules the size of proteins - computational limits mean that practically only a few tens of atoms can be considered. Even semiemprical quantum mechanics, in which approximations and experimental data are introduced, are limited to the consideration of systems the size of a few aminoacids. However, quantum chemistry can be extremely useful in providing parameters for molecular mechanics methods and following chemical reactions in proteins. If you are interested have a look at advanced topic: The application of quantum chemistry to protein simulation..