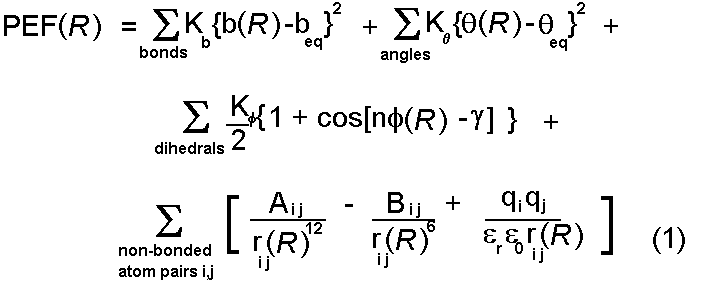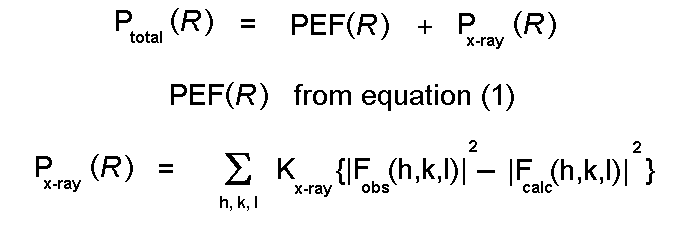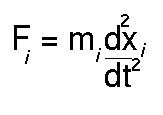Overview of molecular forces: Potential energy functions and simulation methods
Oliver Smart
(c) O.S. Smart
1996, all rights reserved
Back to main PPS course Index
Back to main Molecular Forces index
Back to previous unit The effect of solvent and hydrophobic interactions
Potential energy functions
We have briefly reviewed the variety of interactions which are important
in protein interactions and seen suitable simple mathematical forms
for their representation. These are drawn together to form a potential
energy function:
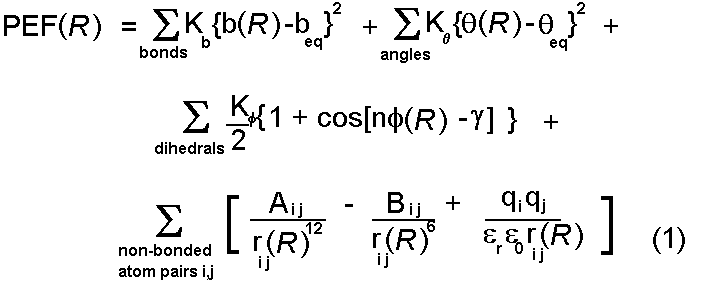
This function can be used to calculate a value for the potential energy
(PEF(R)) for any conformation of a given protein
- defined by the (normally Cartesian) coordinate vector R.
A number of important points
can be made:
- We called the function a "potential" energy function
as it does not contain contributions made to the
total energy made by the motions of the atoms involved.
It is possible to calculate these using molecular
dynamics methods.
- The function aims to give reasonable values for the difference in
"microstate" energies between two different conformations. The
absolute value for the energy given does not mean anything
(certainly NOT the free energy of formation). Only differences
have meaning. The above equation also does not allow the
examination of any process which involves the change in
chemical bonding, e.g., one cannot simulate chemical
reactions in an enzyme active site with it.
- This kind of function is normally of little use in estimating
whether a protein adopts a particular fold - much more useful
is the approach set out by Sippl which uses an empirically based
approach to identify mis-folds. (See Sippl, M.J. (1990)
Calculation of conformational ensembles from potentials of mean force
- an approach to the knowledge-based prediction of local structures
in globular-proteins, J. Mol. Biol. 213:859-883).
- To be able to calculate the potential energy of a protein using the
above equation involves a large number of parameters (equilibrium bond lengths
beq,
bond stretching constants Kb ...). The process of
finding these is arduous and in there are only around four
potential energy functions in common usage for proteins (CHARMm,
AMBER, GROMOS and ECEPP).
- Although results obtained with current potential energy
functions are only approximate they have one great advantage
- they are computationally cheap. This allows the introduction
of realistic representation of environment - such as having
large numbers of explicitly modelled water molecules surrounding
a protein. It also allows the calculation of the potential energy
for many different conformations of the same molecule.
This facilitates the use of techniques such as molecular
dynamics which allows the thermal motions of a system to
be explored. This can be contrasted with quantum chemical
methods which even for small systems are so expensive that
only a limited number of calculations can be made but produce
very accurate energies.
Simulation methods
This section provides a very brief introduction into what the uses
of potential energy functions are in protein studies.
This is in many ways the simplest simulation procedure. The
basic idea is that starting from some structure (R we find its
potential energy using the potential energy function given as
equation (1) above. The coordinate vector R is then varied
using an
optimization procedure
so as to minimize the potential energy PEF(R).
Very often these methods are used if a distorted structure is
produced - e.g. a homology based model. Energy minimization
can then relieve short interatomic distances while maintaining
important structural features.
Energy minimization can be used to help to solve experimental structures:
Extensive notes on optimization procedures are
available
from the M.Sc.
Molecular Modelling and Bioinformatics at Birkbeck.
In molecular dynamics studies the motion of a molecule is simulated as a function
of time. A simple description is that Newton's second law of motion:
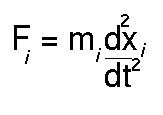
is solved to find how the position for each atom of the system
xi varies with t. To find the forces
on each atom (Fi) the derivative vector (or gradient) of
equation 1 is calculated. Factors such as the temperature and pressure
of the system can be included in the treatment.
Molecular dynamics simulation procedures are very popular in the protein field.
They have the advantage that they can treat systems where motion is essentially
diffusive in character - important because of the role of water in
protein structure. The procedures can be used to calculate "ensemble
average" properties - recent advances have included the ability to calculate
free energy differences between (slightly) different ligands or conformations
of a protein. A disadvantage of conventional molecular dynamics procedures is that
they can only tackle motions with a relatively short time scale - one nanosecond
is the approximate upper limit with current computers.
Very many other methods use potential energy functions for the study of
proteins conformation and dynamics. An example of this is the
Path Energy Minimization procedure - which aims to
find routes for large scale conformational transitions of proteins
(developed by the author of this section of the course).
Bibliography
Useful sources of information to start to learn more about this topic:
-
S.J. Weiner, P.A. Kollman, D.A. Case, U.C. Singh, G. Alagona,
S. Profeta Jr. and P. Weiner. "A new force field for the molecular
mechanical simulation of nucleic acids and proteins".
J. Am. Chem. Soc. , 106:765-784 (1984).
- The original paper describing the AMBER potential energy function. An
interesting if slightly heavy going paper describing the process of
developing an energy function, source of parameters etc..
For further details of the AMBER program and energy function then
why not look at the
AMBER home page at the University of Calfornia, San Francisco.
Back to previous unit The effect of solvent and hydrophobic interactions
Back to the Top