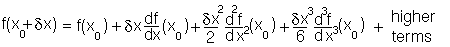
Back to main Molecular Forces index
Back to main PPS course Index
From high school mathematics any function minimum can be expanded as a Taylor power series:
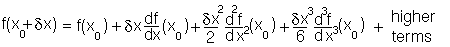
Consider using this expansion for the potential energy for bond deformation
around the equilibrium value. The term in
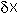 will be zero
because the derivative of the potential must be zero at an equilibrium value.
Close to the equilibrium (at low values of
will be zero
because the derivative of the potential must be zero at an equilibrium value.
Close to the equilibrium (at low values of 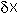 ) the term in
) the term in 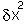 will increasingly
tend to dominate the term in
will increasingly
tend to dominate the term in 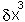 and higher terms. The practical upshot of this is that any function
which varies around a minimum will behave as a quadratic sufficiently
close to the minimum. i.e., in the case above the function will be:
and higher terms. The practical upshot of this is that any function
which varies around a minimum will behave as a quadratic sufficiently
close to the minimum. i.e., in the case above the function will be:
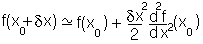
so it will behave as a harmonic function:
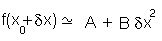 with A and B as constants. This approach is similar to the theoretical basis of many of the methods used in
energy minimization.
with A and B as constants. This approach is similar to the theoretical basis of many of the methods used in
energy minimization.
In deriving a potential energy function for a molecule we are not
interested in the absolute value of the potential energy so that the first term is unimportant.
Therefore a Hooke's Law expression is normally used for the potential energy cost of bond
deformation:
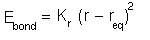
The simple expression means that only one constant has to be found for each different type of bond. However, it is only a first order approximation and if more accuracy is required then higher moments can be invoked or the Morse potential can be used.
The same reasoning also holds true for other terms which represent the energy cost for the change in a coordinate which only varies by a small amount around an equilibrium value ( e.g., bond angles). However, if the coordinate can take a variety of values then such an approach is unsuitable (eg., dihedral angles have more than one stable value and must be included in a different way).
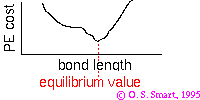
As a practical example consider a bond whose potential is modelled by the Morse potential.
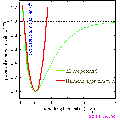 (Click on icon to proper sized image).
(Click on icon to proper sized image).
The Morse potential is given by:
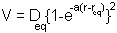
the minimum of the function is at 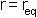 i.e. the equilibrium bond length (see graph above). It can be shown that (a little exercise to keep that high school maths fresh!) the second differential of the potential at the equilibrium position is:
i.e. the equilibrium bond length (see graph above). It can be shown that (a little exercise to keep that high school maths fresh!) the second differential of the potential at the equilibrium position is:
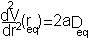
plugging this into the harmonic equation above we achieve the red line shown in the graph. The parabola is a good approximation to Morse potential close to the equilibrium but begins to deviate away from this position. In particular the potential energy of parabola tends to infinity at large distances whereas the Morse potential can provide a more realistic representation of the formation energy of the bond.
Back to main Molecular Forces index
Back to main PPS course Index